1纳米等于多少a°-中考冲刺数学试题1含答案解析

免费进学习资料群！

以微课堂学习群

奥数国家级教练与四名特级

教师联手执教。

一．选择题（共10小题，满分40分，每小题4分）

1．（4分）若数a、b满足a+b＝0，则a、b两数必满足的是（）

A．两数相等 B．均等于0 C．互为相反数 D．互为倒数

2．（4分）下列运算正确的是（）

A．x2+x3＝x5 B．a6÷a3＝a2

C．（﹣2a2）3＝﹣8a6 D．（a+b）2＝a2+b2

3．（4分）1纳米＝10﹣9米，有一种病毒的直径为25100纳米，请用科学记数法表示该病毒的直径（）

A．25.1×106米 B．2.51×10﹣5米

C．0.251×10﹣4米 D．25.1×10﹣4米

4．（4分）如图是由棱长为1的几个正方体组成的几何体的三视图，则这个几何体的体积是（）

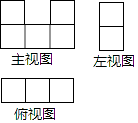
A．3 B．4 C．5 D．6

5．（4分）在一次信息技术考试中，某兴趣小组8名同学的成绩（单位：分）分别是：7、10、9、8、7、9、9、8，则这组数据的众数和中位数是（）

A．9、8.5 B．7、9 C．8、9 D．9、9

6．（4分）如图，将一张含有30°角的三角形纸片的两个顶点叠放在长方形纸条的两条对边上，若∠2＝50°，则∠1的度数为（）

A．10° B．15° C．18° D．20°

7．（4分）如图，点A，B在反比例函数y

（x＞0）的图象上，点C，D在反比例函数y

（k＞0）的图象上，AC∥BD∥y轴，已知点A，B的横坐标分别为1，2，△OAC与△ABD的面积之和为

，则k的值为（）

A．4 B．3 C．2 D．

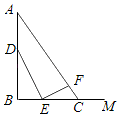
8．（4分）如图，AB＝4，射线BM和线段AB互相垂直，D为线段AB上一点，点E在射线BM上，且2BE＝DB，作EF⊥DE，并截取EF

DE，连接AF并延长交射线BM于点C，设BE＝x，BC＝y，则（）

A．

B．

C．

D．

9．（4分）甲、乙两人沿同一公路从A地出发到B地，甲乘汽车，乙骑摩托车，从A地到B地的路程为120千米．若图中CD，OE分别表示甲、乙离开A地的路程S（千米）和时间t（小时）的函数关系的图象，则下列结论中错误的是（）

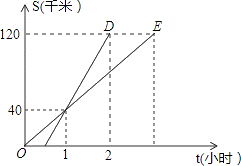
A．甲的速度为60千米/小时

B．乙从A地到B地用了3小时

C．甲比乙晚出发0.5小时

D．甲到达B地时，乙离A地80千米

10．（4分）如图，在矩形ABCD中，AB＝8，AD＝6，动点P满足S△PAB

S矩形ABCD，则点P到A、B两点的距离之和PA+PB的最小值为（）

A．10 B．8

C．8

D．8

二．填空题（共4小题，满分20分，每小题5分）

11．（5分）在实数范围内可以把x2﹣6分解因式为 ．

12．（5分）命题：“如果a＝b，那么3a＝3b”的逆命题是 ，该逆命题是 （填“真”或“假”）命题．

13．（5分）如图，四边形ABCD内接于⊙O，∠A＝125°，则∠C的度数为 ．

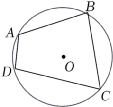
14．（5分）已知抛物线y＝ax2+bx+c与x轴交于A（﹣1，0），B（5，0），则一元二次方程ax2+bx+c＝0的根是 ．

三．解答题（共2小题，满分16分，每小题8分）

15．（8分）计算：（﹣1）2019+tan60°﹣2﹣1+（3.14﹣π）0．

16．（8分）列方程解应用题：某蔬菜公司的一种绿色蔬菜，若在市场上直接销售，每吨利润为1000元，经粗加工后销售，每吨利润可达4500元，经精加工后销售，每吨利润涨至7500元，当地一家公司收购这种蔬菜140t，该公司的加工生产能力是：如果对蔬菜进行粗加工，每天可加工16t，如果进行精加工，每天可加工6t，但两种加工方式不能同时进行，受季节等条件限制，公司必须在15天将这批蔬菜全部销售或加工完毕，为此公司研制了三种可行方案：

方案一：将蔬菜全部进行粗加工．

方案二：尽可能多地对蔬菜进行精加工，没来得及进行加工的蔬菜，在市场上直接销售．

方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好15天完成．

你认为哪种方案获利最多？为什么？最多可获利多少元？

四．解答题（共2小题，满分16分，每小题8分）

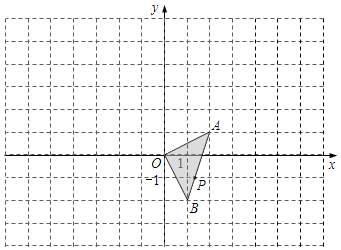
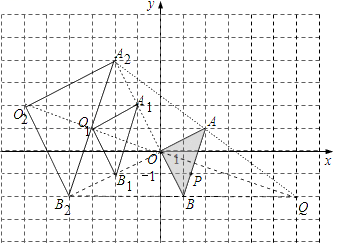
17．（8分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，1）、O（0，0）、B（1，﹣2），P（a，b）是△AOB的边AB上一点．

（1）画出将△AOB向左平移3个单位，再向上平移1个单位后的△A1O1B1，并分别写出点A、P的对应点A1、P1的坐标；

（2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出将△A1O1B1放大后的△A2O2B2，并分别写出点A1、P1的对应点A2、P2的坐标；

（3）判断△AOB与△A2O2B2，能否是关于某一点Q为位似中心的位似图形，若是，请在图中标出位似中心Q，并写出点Q的坐标．

18．（8分）用灰白两种颜色的正方形地砖，按如下所示的规律拼成图案：

（1）第4个图案有白色地砖多少块？第n个图案呢？

（2）已知每个小正方形的边长均为0.8m，若学校用第n个图案铺设长为64.8m的长廊，则需要灰色地砖多少块？

五．解答题（共2小题，满分20分，每小题10分）

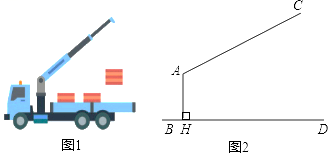
19．（10分）2018年12月5日，备受关注的郑州奥体中心“一场两馆”主体结构已完成，装饰装修完成85%，据了解，郑州奥体中心将作为2019年在郑州市举办的第十一届全国少数民族传统体自运动会主办场地，包括“一场两馆”，即6万个座位的体育场、1.6万个座位的体育馆和3000和座位的游泳馆，图1是装饰现场一辆吊车的实物图，图2是其工作示意图，AC是可以伸缩的起重臂，其转动点A离地面BD的高度AH为3.4m，当起重臂AC长度为9m，张角∠HAC为118°时，求操作平台C离地面的高度．（结果保留小数点后一位参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）

20．（10分）如图，四边形ABCD内接于⊙O，AC平分∠BAD，延长DC交AB的延长线于点E．

（1）若∠ADC＝78°，求∠CBE的度数；

（2）若AC＝EC，求证：AD＝BE．

六．解答题（共1小题，满分12分，每小题12分）

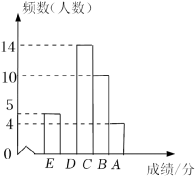
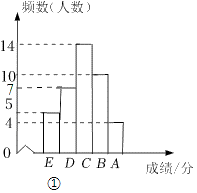
21．（12分）在加强对中小学生”双减”和“五项管理”政策下，某校为了了解在教学改革模式下九年级期末数学成绩，随机抽取40名学生抽测，满分为50分，并将测试成绩分成五档：A档：40≤x≤50；B档：30≤x＜40；C档：20≤x＜30；D档：10≤x＜20；E档：0≤x＜10，绘制频数分布图如下，已知在20≤x＜30这一组的具体得分（单位：分）是20、26、22、27、28、26、26、26、24、29、27、21、28、27．

（1）在20≤x＜30这一组成绩数据中，中位数为，众数为，并补全频数分布直方图；

（2）若成绩不低于40分为优秀，该校九年级有1800名学生，则该校九年级期末数学成绩优秀的学生约有多少名？

（3）该校举办“一帮一”活动，在A档中随抽取两名学生，在E档随抽取两名学生，则该4同学中随机抽取2名学生，恰好抽出一名A档学生和一名E档学生的概率是多少？

七．解答题（共1小题，满分12分，每小题12分）

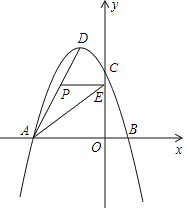
22．（12分）如图所示，在平面直角坐标系中，抛物线y＝ax2+bx+3经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，连接AD，点P是线段AD上一个动点（不与A，D重合），过点P作y轴的垂线，垂足点为E，连接AE．

（1）求抛物线的函数解析式，并写出顶点D的坐标；

（2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值．

八．解答题（共1小题，满分14分，每小题14分）

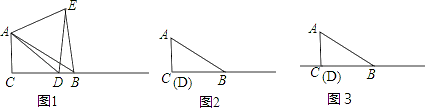
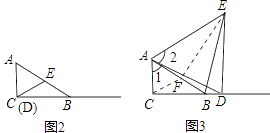
23．（14分）问题：如图1，在Rt△ABC中，∠C＝90°，∠ABC＝30°，点D是边CB上任意一点，△ADE是等边三角形，且点E在∠ACB的内部，连接BE．探究线段BE与DE之间的数量关系，请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．

（1）当点D与点C重合时（如图2），请你补全图形．由∠BAC的度数为 ，点E落在 ，容易得出BE与DE之间的数量关系为 ；

（2）当点D是BC上任意一点（不与点B，C重合）时，结合图1，研究（1）中线段BE与DE之间的数量关系是否与成立，并证明你的结论；

（3）如图3，在直线BC上有一点P，使△PAB为等腰三角形，请找出这样的点P，并直接写出∠APB的度数．

参考答案与试题解析

一．选择题（共10小题，满分40分，每小题4分）

1．【解答】解：∵a+b＝0，

∴a，b互为相反数，

故选：C．

2．【解答】解：A．x2+x3无法合并，故此选项不合题意；

B．a6÷a3＝a3，故此选项不合题意；

C．（﹣2a2）3＝﹣8a6，故此选项符合题意；

D．（a+b）2＝a2+2ab+b2，故此选项不合题意；

故选：C．

3．【解答】解：25100纳米用科学记数法表示该病毒的直径为25100×10﹣9＝2.51×10﹣5米．

故选：B．

4．【解答】解：由该几何体的三视图知小正方体的分布情况如下：

则该几何体的体积为5×13＝5，

故选：C．

5．【解答】解：把这组数据重新排序后7，7，8，8，9，9，9，10，

∴这组数据的中位数（8+9）÷2＝8.5，

∵9是这组数据中出现次数最多的数据，

∴这组数据的众数为9；

故选：A．

6．【解答】解：如图：

∵矩形的对边平行，∠2＝50°，

∴∠2＝∠3＝50°，

根据三角形外角性质，可得∠3＝∠1+30°，

∴∠1＝50°﹣30°＝20°，

故选：D．

7．【解答】解：∵点A，B在反比例函数y

（x＞0）的图象上，点A，B的横坐标分别为1，2，

∴点A的坐标为（1，1），点B的坐标为（2，

），

∵AC∥BD∥y轴，

∴点C，D的横坐标分别为1，2，

∵点C，D在反比例函数y

（k＞0）的图象上，

∴点C的坐标为（1，k），点D的坐标为（2，

），

∴AC＝k﹣1，BD

，

∴S△OAC

（k﹣1）×1

，S△ABD

•

（2﹣1）

，

∵△OAC与△ABD的面积之和为

，

∴

，

解得：k＝3．

故选：B．

8．【解答】解：作FG⊥BC于G，

∵∠DBE＝∠EGF＝90°，∠BDE＝∠FEG，

∴△DBE∽△EGF，

∴

，

∵

，2BE＝DB，BE＝x，

∴FG

BE

x，EG

DB＝x，

∵FG∥AB，

∴

，

∴

，

整理得，

．

故选：A．

9．【解答】解：设甲的解析式为y＝kx+b，可得：

，

解得：

，

所以解析式为：y＝80x﹣40，

把y＝0代入解析式中，可得：0＝80x﹣40，

解得：x＝0.5，

所以甲的速度为：120÷（2﹣0.5）＝80，故A错误；

由图象可得乙的速度为：40÷1＝40，所以乙的时间为：120÷40＝3小时，故B正确；

甲比乙晚0.5小时，故C正确；

甲到达B地时，乙离A地2×40＝80千米，故D正确；

故选：A．

10．【解答】解：设△ABP中AB边上的高是h．

∵S△PAB

S矩形ABCD，

∴

AB•h

AB•AD，

∴h

AD＝4，

∴动点P在与AB平行且与AB的距离是4的直线l上，

如图，作A关于直线l的对称点E，连接AE，BE，则BE的长就是PA+PB的最小值．

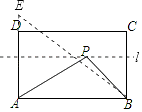
在Rt△ABE中，∵AB＝8，AE＝4+4＝8，

∴BE

，

即PA+PB的最小值为8

．

故选：C．

二．填空题（共4小题，满分20分，每小题5分）

11．【解答】解：x2﹣6＝（x

）（x

），

故答案为：（x

）（x

）．

12．【解答】解：根据题意得：命题“如果a＝b，那么3a＝3b”的条件是如果a＝b，结论是3a＝3b，故逆命题是如果3a＝3b，那么a＝b，该命题是真命题．

故答案为：如果3a＝3b，那么a＝b，真．

13．【解答】解：∵四边形ABCD内接于⊙O，

∴∠A+∠C＝180°，

∵∠A＝125°，

∴∠C＝180°﹣125°＝55°，

故答案为：55°．

14．【解答】解：∵抛物线y＝ax2+bx+c与x轴交于A（﹣1，0），B（5，0），

∴当y＝0时，0＝ax2+bx+c对应的x的值﹣1或5，

∴一元二次方程ax2+bx+c＝0的根是x1＝﹣1，x2＝5，

故答案为：x1＝﹣1，x2＝5．

三．解答题（共2小题，满分16分，每小题8分）

15．【解答】解：（﹣1）2019+tan60°﹣2﹣1+（3.14﹣π）0

＝﹣1

．

16．【解答】解：方案三获利最多，

理由：∵粗加工需的天数为：140÷16＝8

，

∴按照方案一可以获得利润：140×4500＝630000（元）；

∵精加工15天可以加工：15×6＝90（吨），

∴按照方案二可以获得利润：90×7500+（140﹣90）×1000＝725000（元），

设粗加工x天，则精加工（15﹣x）天，

由题意可得：16x+6（15﹣x）＝140，

解得x＝5，

∴15﹣x＝10，

∴按照方案三可以获得利润：16×5×4500+6×10×7500＝810000（元），

答：最多可获利810000元．

四．解答题（共2小题，满分16分，每小题8分）

17．【解答】解：（1）如图，△A1O1B1即为所求，A1（﹣1，2），P1（a﹣3，b+1）；

（2）如图，△A2O2B2即为所求，A2（﹣2，4），P2（2a﹣6，2b+2）；

（3）△AOB与△A2O2B2是关于点Q（6，﹣2）为位似中心的位似图形．

18．【解答】解：（1）第一个图案中共有白色地砖8块，即5×1+3，

第二个图案中共有白色地砖13块，即5×2+3，

第三个图案中共有白色地砖18块，即5×3+3，

…

∴第四个图案中共有白色地砖5×4+3＝23块，

第n个图案中共有白色地砖（5n+3）块；

（2）根据题意得0.8（2n+1）＝64.8，

解得n＝40，

∴需要灰色地砖40块．

五．解答题（共2小题，满分20分，每小题10分）

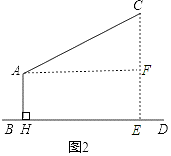
19．【解答】解：作CE⊥BD于E，AF⊥CE于F，如图2，

则四边形AHEF为矩形，

∴EF＝AH＝3.4m，∠HAF＝90°，

∴∠CAF＝∠CAH﹣∠HAF＝118°﹣90°＝28°，

在Rt△ACF中，∵sin∠CAF

，

∴CF＝9sin28°＝9×0.47＝4.23，

∴CE＝CF+EF＝4.23+3.4≈7.6（m），

答：操作平台C离地面的高度约为7.6m．

20．【解答】（1）解：∵四边形ABCD内接于⊙O，

∴∠ADC+∠ABC＝180°，

∵∠CBE+∠ABC＝180°，

∴∠CBE＝∠ADC＝78°；

（2）证明：∵AC平分∠BAD，

∴∠DAC＝∠BAC，

∵AC＝EC，

∴∠E＝∠BAC，

∴∠DAC＝∠E，

在△ADC和△EBC中，

，

∴△ADC≌△EBC（AAS），

∴AD＝BE．

六．解答题（共1小题，满分12分，每小题12分）

21．【解答】解：（1）在20≤x＜30中有14个数据，从小到大排列为：20、21、22、24、26、26、26、26、27、27、27、28、28、29，

中间两个数是26、26，

∴中位数：26，

众数：26，

∵10≤x＜20的数一共有：40﹣4﹣10﹣14﹣5＝7，

作图①如下：

（2）不低于40分的频率：

100%＝10%，

∴九年级期末数学成绩优秀的学生约有：1800×10%＝180（名），

答：九年级期末数学成绩优秀的学生约有180名；

（3）设在A档中随抽取两名学生分别为a，b，在E档随抽取两名学生分别为m、n，由题意列表如下：

共有12中可能，恰好抽出一名A档学生和一名E档学生的可能性有8种，

∴恰好抽出一名A档学生和一名E档学生的概率：P

．

答：恰好抽出一名A档学生和一名E档学生的概率是

．

七．解答题（共1小题，满分12分，每小题12分）

22．【解答】解：（1）∵抛物线y＝ax2+bx+3经过A（﹣3，0）、B（1，0）两点，

∴

，解得

，

∴抛物线的解析式为y＝﹣x2﹣2x+3；

∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，

∴抛物线的顶点坐标D为（﹣1，4）；

（2）设AD为解析式为y＝kx+b，

把点A（﹣3，0），D（﹣1，4）代入得

，解得

，

∴直线AD的解析式为y＝2x+6；

设P（x，2x+6），则E（0，2x+6），

∴S

•（﹣x）•（2x+6）

＝﹣x2﹣3x（﹣3＜x＜﹣1），

∵S＝﹣（x

）2

，

∴当x

时，S有最大值，最大值为

．

八．解答题（共1小题，满分14分，每小题14分）

23．【解答】解：（1）如图2，

∵∠C＝90°，∠ABC＝30°，

∴∠BAC＝60°，

∵△ADE是等边三角形，

∴AE＝CE，

∴点E落在AB的中点处；

∴AE＝CE＝BE＝DE，

故答案为：60°；AB的中点处；BE＝DE；

（2）如图3．

猜想：BE＝DE．

证明：取AB的中点F，连接EF．

∵∠ACB＝90°，∠ABC＝30°，

∴∠1＝60°，CF＝AF

AB，

∴△ACF是等边三角形．

∴AC＝AF ①

∵△ADE是等边三角形，

∴∠2＝60°，AD＝AE②

∴∠1＝∠2．

∴∠1+∠BAD＝∠2+∠BAD．

即∠CAD＝∠FAE③

由①②③得△ACD≌△AFE（SAS）．

∴∠ACD＝∠AFE＝90°．

∵F是AB的中点，

∴EF是AB的垂直平分线，

∴BE＝AE，

∵△ADE是等边三角形，

∴DE＝AE，

∴BE＝DE；

（3）如图4，

∵△PAB为等腰三角形，

∴①当AP＝AB时，即：AP1＝AB，

∴∠AP1B＝∠ABP1＝30°，

②当BP＝AB时，

Ⅰ、BP2＝AB，

∴∠AP2B

（180°﹣∠ABC）＝75°，

Ⅱ、BP4＝AB，

∴∠BAP4＝∠AP4B

∵∠ABC＝30°＝∠BAP4+∠AP4B

∴∠AP4B＝15°

③当AP＝BP时，即：AP3＝BP3，

∴∠BAP3＝∠ABC＝30°，

∴∠AP3B＝180°﹣∠ABC﹣∠BAP3＝120°，

即：∠APB的度数为15°，30°，75°，120°．

免费进学习资料群！

以微课堂学习群

奥数国家级教练与四名特级

教师联手执教。

温馨提示

创业/副业必备：

本站已持续更新1W+创业副业顶尖课程，涵盖多个领域。

点击查看详情