三角形重心的性质-三角形的五心：内心外心重心垂心旁心全解析，再也不会搞混了

三角形的五心，很多同学非常容易混淆，今天我们专门详细系统的讲解一下这五心的要点和区别，希望能够对你有所帮助。

来看知识要点

一、三角形的内心：

1.定义：三角形的内切圆圆心称为内心。

2.性质1.三角形的内心是三角形的三条内角平分线的交点。

性质2.为三角形的内心的充要条件是到三角形三边的距离相等。

性质3.设I为三角形ABC内一点，AI所在直线交三角形ABC外接圆于D，则I为三角形ABC内心的充要条件是：ID=DB=DC。（俗称“鸡爪定理”）

3.典型例题：

二、三角形的外心：

1.定义：三角形的外接圆圆心称为外心

2.性质1.三角形的外心是三角形三条边的垂直平分线交点（反过来只需要两条）。

性质2.三角形所在平面内的一点是其外心的充要条件是：该点到三顶点的距离相等。

性质3.直角三角形的外心是斜边的中点；锐角三角形的外心在三角形的内部；钝角三角形的外心在三角形的外部。

3.典型例题

三、三角形的重心‬

1.定义：三角形三条中线的交点称为三角形的重心。

2.性质

3.典型例题

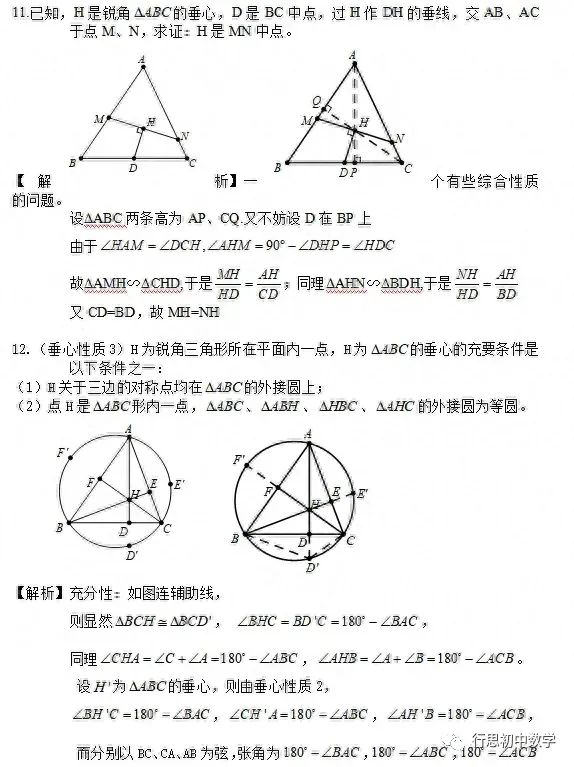
四‬、三角形的垂心

1.定义：三角形三边上的高线的交点称为三角形的垂心。

2.性质：

性质1. 直角三角形的垂心在直角顶点，锐角三角形的垂心在形内，钝角三角形的垂心在形外。

3.典型例题

五、三角形的旁心

1.定义：三角形的旁切圆（与三角形的一边和其他两边的延长线都相切的圆）的圆心，称为三角形的旁心。

2.性质：

性质1. 三角形一内角平分线和另外两顶点处的外角平分线交于一点，该点即是旁心。

性质2.旁心到三边的距离相等，每个三角形都有三个旁心。

3.典型例题

讲解，353道变式跟踪练习，题型全覆盖，提分无忧

再来看针对性练习，及时巩固：

创业/副业必备：

本站已持续更新1W+创业副业顶尖课程，涵盖多个领域。

点击查看详情