

音乐是一个很奇妙的东西,它无体无身,但它总是可以调节人们的情绪!
数涵妙理总堪寻,道通功成浅亦深!大家好,我是麒麟子,我和我的数学故事都还在路上!

向量+三角形前情回顾
关于平面向量和三角形相结合的内容,其实一直以来就是比较热门的出题方向,前面我们给大家分享了一道经典的例题:

这道题目主要讨论的是三角形的“外心”和“垂心”的性质:
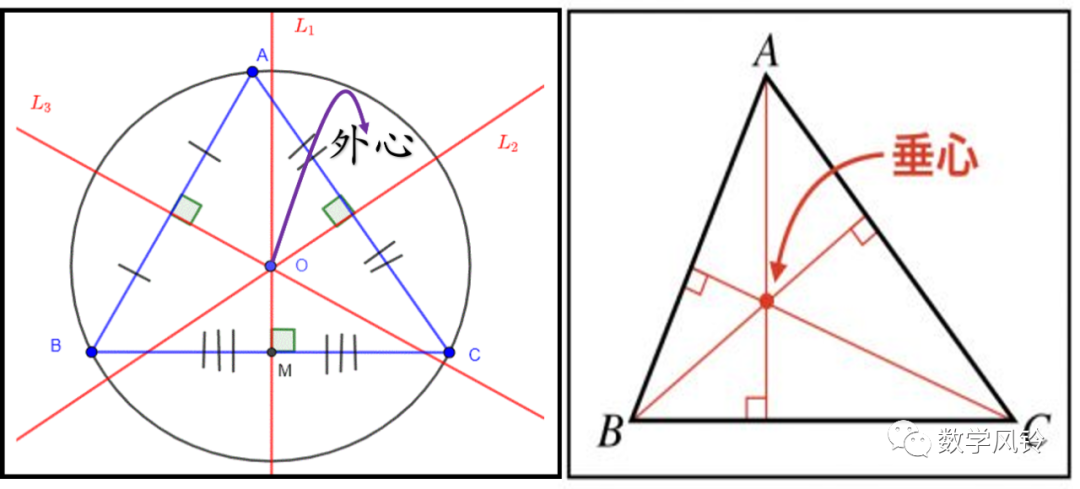
通过对那道题目的证明我们还得到了一个有用的结论:
其实如果你认真钻研过这道题目,你会从中积累到很多有用的向量知识,后续遇到相关的题目,就会有对应的处理思路,这就是我们积累知识的过程,做一道题目,积累一些有用的知识。上述例题内容回顾点击下方蓝色链接:
向量+三角形重心
我们本期来给大家分享2道平面向量和三角形的另一道经典例题,这道题目主要考察的是向量和三角形重心,重心是三角形中另一个非常重要的知识点,和垂心、外心一样,重心也有很多值得研究的性质。
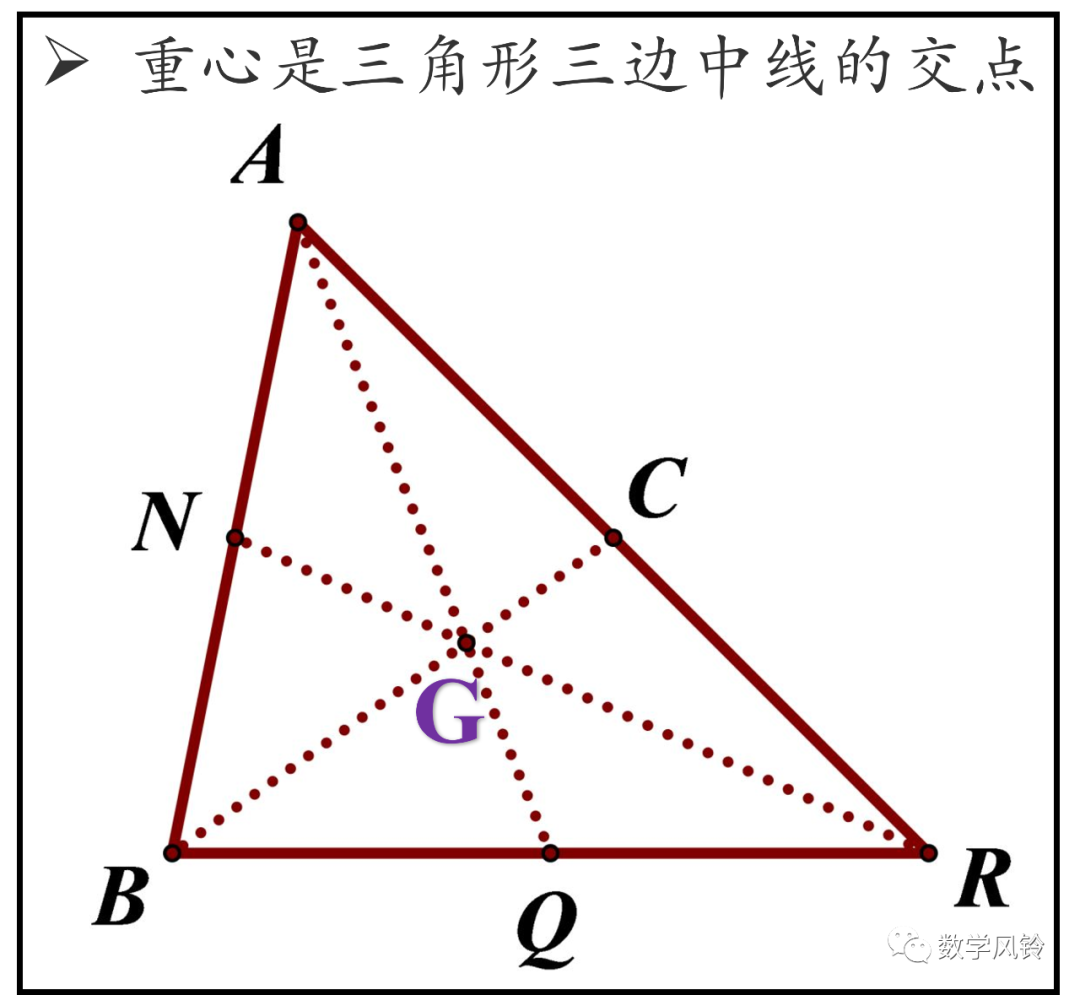
今天讨论的两道题目本质上就是平面向量和三角形重心的综合考察,这是我对于向量和三角形综合考察部分的又一次丰富,这两道题目的含金量也比较高,也会衍生出相应的公式结论,都是我们积累的素材。通过这2道题目的训练,能让大家学到很多有用的数学知识和数学技巧,建议和之前外心垂心那篇文章结合起来学习:
例题分析
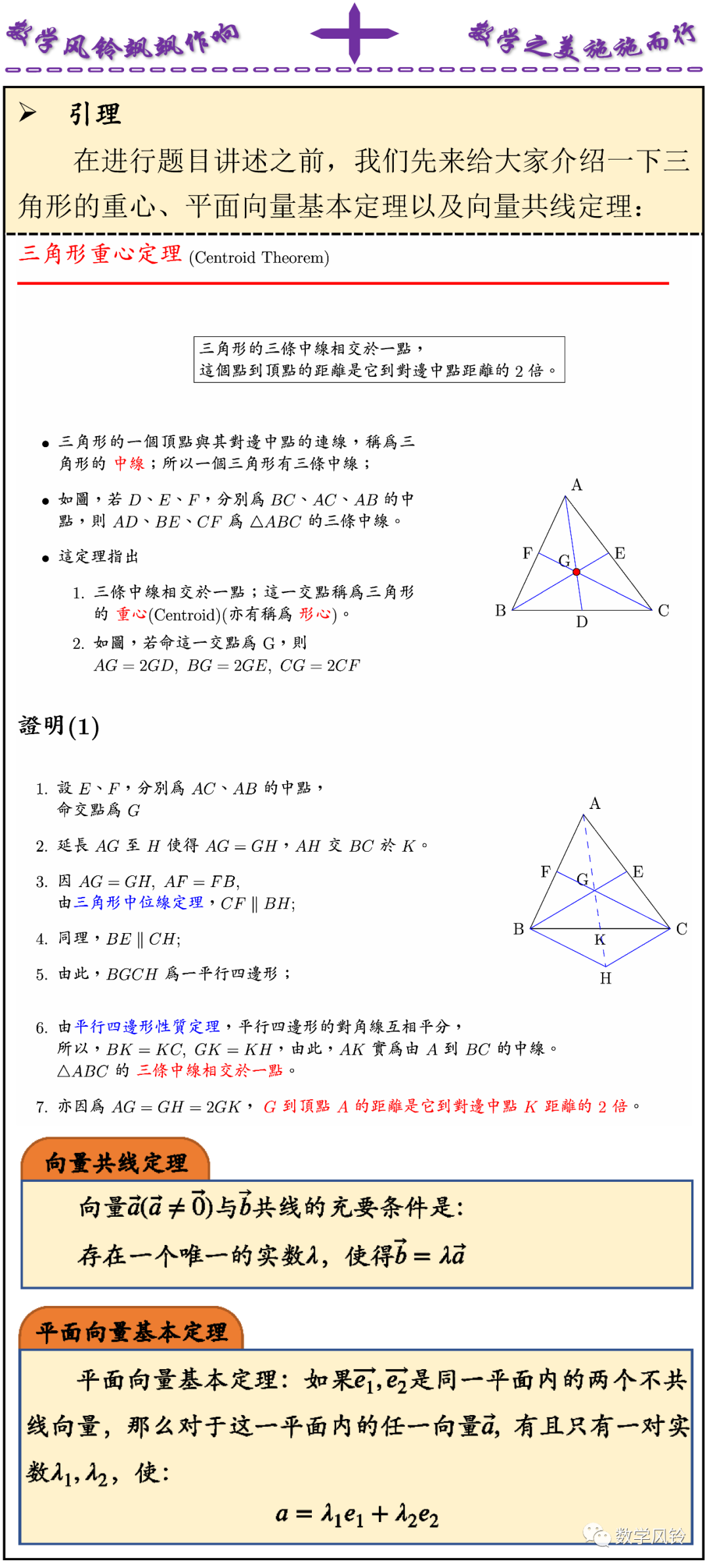

总结
【题目定位】
这2道平面向量题目立足于向量的基本知识点,同时综合了三角形重心的相关性质,属于中等难度,在分析的过程中,无非是对于向量部分相关定理的应用,三角形重心具有许多性质,在这2道题目中也有呈现,实现了向量和三角形的巧妙结合,题目的结果也是实际中比较常用的一些结论,非常有价值。
【题目分析】
第一道题目首先是基于向量共线定理,对具体向量进行表示,之后结合图形、向量的加减运算以及三角形重心的性质对涉及到向量进行表示,接着进行整理,最后应用平面向量基本定理列出参数满足的方程,得出结论。
第二道题目基于三角形重心的性质对向量进行表示,之后基于向量的运算法则转化为题目中给定的基底向量即可。
好文推荐
推荐大家阅读的6篇高质量文章:
第一篇文章我以金庸武侠为载体给大家讲述了“函数”的本质;
第二篇文章我给大家讲述了指数函数、对数函数、幂函数三者源于同样一个简洁的表达式,三者本自同根生。
第三篇文章我给大家详细讲述了一道非常经典的导数题目,用两种思路不同的解法,涉及到导数中许多常用的核心方法,是一篇很好的导数提升文章!
第四篇文章通过一道新颖题型给大家讲述了立体几何中的多面体欧拉定理,算是对立体几何内容进行一个有趣的拓展。
第五篇文章给大家讲了指数幂的一点历史,帮助大家好理解指数函数!
第六篇文章给大家总结了2022届的《八省联考》以及备考经验!
(点击下方蓝色链接)

一门科学,只有当它成功地运用数学时,才能达到真正完善的地步。
——卡尔·马克思 德国政治家和思想家
创业/副业必备:
本站已持续更新1W+创业副业顶尖课程,涵盖多个领域。
点击查看详情


评论(0)